Вы используете устаревший браузер. Этот и другие сайты могут отображаться в нём некорректно.
Вам необходимо обновить браузер или попробовать использовать другой.
Вам необходимо обновить браузер или попробовать использовать другой.
Квантовые компьютеры наступают?
- Автор темы Mike22
- Дата начала
Компания D-Wave (смотрите самый первый пост в теме) живёт!
И дожила до того, что объявила о начале продаж первого в мире серийного квантового компьютера на 128 кубит.
Первым покупателем стала Lockheed Martin.
Интересно, кто купит второй
http://www.dwavesys.com/en/products-services.html
И дожила до того, что объявила о начале продаж первого в мире серийного квантового компьютера на 128 кубит.
Первым покупателем стала Lockheed Martin.
Интересно, кто купит второй
http://www.dwavesys.com/en/products-services.html
Аццкий Минус
стальной крыс на сафари
где там написано Lockheed?
http://www.dwavesys.com/en/pressreleases.htmlгде там написано Lockheed?
Называют и стоимость компьютера - $10 млн.
http://www.engadget.com/2011/05/18/d-wave-one-claims-mantle-of-first-commercial-quantum-computer/
Аццкий Минус
стальной крыс на сафари
http://www.gamer.ru/everything/d-wave-prodala-pervyy-kvantovyy-kompyuter
"Официальный пресс-релиз больше похоже на сообщение о заключении контракта о долгосрочном сотрудничестве, по которому специалисты D-Wave должны разработать... ничего, о чём можно было бы сейчас сообщить. Вся информация находится в закрытом доступе."
"Официальный пресс-релиз больше похоже на сообщение о заключении контракта о долгосрочном сотрудничестве, по которому специалисты D-Wave должны разработать... ничего, о чём можно было бы сейчас сообщить. Вся информация находится в закрытом доступе."
Аццкий Минус
стальной крыс на сафари
и, похоже, слегка поторопилась - на пороге качественно новая технология...Первым покупателем стала Lockheed Martin.
http://www.gazeta.ru/science/2011/08/11_a_3729821.shtml
"— 11.08.11 15:31 —
...впервые удалось запутать квантовые состояния двух атомов с помощью микроволн, что в перспективе позволит радикально уменьшить размер квантовых вычислительных устройств, работающих на основе лазеров и занимающих сейчас целую комнату.
...как оптимистично полагают физики из американского Национального института стандартов и технологий (НИСТ), лазерный блок установки может быть уменьшен до размера устройств, применяемых в портативных DVD-плеерах. По сравнению со сложными, дорогими и громоздкими лазерами, которые используют для спутывания ионов, микроволновая электроника более дешевая, намного более компактная, а главное, легко масштабируемая, что позволит создавать промышленные платформы для спутывания тысяч атомов."
http://www.lektorium.tv/course/?id=22805А кроме шифрования эта технология где-нибудь применима?
Создан первый в мире оптический программируемый процессор (чип) для квантовых вычислений.
http://www.extremete...m-photonic-chip
перевод от Google - http://translate.goo...ic-chip&act=url
http://www.extremete...m-photonic-chip
перевод от Google - http://translate.goo...ic-chip&act=url
Сюрпризы квантовой топологии

04 ноября 2015 Бёрд Киви
Топологический квантовый компьютер пока что никто сделать не сумел. Но суть идей в основе этой концепции необычайно красива, а практические успехи на пути её освоения уже несомненны. Так что в итоге наверняка все должно получиться
Сюрпризы начинаются
В принципе, данный материал вполне можно было бы озаглавить «Другая физика». Потому что весь набор результатов, получаемых в процессе освоения области с громким названием «топологические квантовые вычисления» – это, по сути дела, тихая, незаметная и одновременно великая научная революция.

Если приглядеться, то в данном направлении буквально каждый шаг – от истории зарождения и вплоть до новейших достижений – хотя бы чуть-чуть (а порою существенно) изменяет и переворачивает устоявшиеся научные представления об устройстве окружающего мира. Но поскольку происходит это все очень постепенно, никто как бы не замечает, что вся физика тоже попутно переворачивается — с головы на ноги.
Ну а чтобы столь важный процесс стал не только заметным, но и вполне понятным, рассказывать историю надо в общей исторической ретроспективе. Однако начать лучше все же с самых последних новостей – для общего представления о ситуации в столь интересной области и о масштабе происходящих перемен.
Пять тысяч и 50 миллионов
Ежегодно 8 августа – в день рождения П. А. М. Дирака – мировая наука отмечает наиболее выдающиеся достижения в сфере теоретической физики. По давно заведенной традиции, лауреатов очередной Медали Дирака принято выбирать среди тех теоретиков, которым еще не довелось получить Нобелевскую премию. И хотя сопутствующий денежный приз совсем невелик, всего 5 тысяч евро, медаль Дирака считается в физическом сообществе весьма престижной и почетной наградой.

Чаще всего этот приз достается исследователям, занимающимся либо физикой частиц высоких энергий и теорией струн, либо космологией и теорией инфляции (считается, что именно там проходят передовые рубежи физической науки). Однако в нынешнем году медалью Дирака было решено наградить трех ученых, известных по своим работам в области физики конденсированных сред, – Алексея Китаева, Грегори Мура и Николаса Рида. Как сказано в официальном представлении к награде, «за их междисциплинарные вклады, обеспечившие введение концепций конформной теории поля и статистики неабелевых квазичастиц в системы конденсированной материи и применение этих идей к квантовым вычислениям. Работы этих ученых сыграли фундаментальную роль для последних успехов в нашем понимании квантовых состояний материи и квантовой сцепленности. А также породили интенсивный экспериментальный поиск квазичастиц Майораны – возбуждений материи, действующих как своя собственная античастица...»
Для обычных людей, далеких от высоких сфер теоретической физики и не владеющих профессиональной терминологией, подобные разъяснения не объясняют практически ничего. К великому сожалению. Потому что на самом деле речь тут идет о вещах, которые, во-первых, ничуть не менее важны для науки, чем Большой адронный коллайдер или теория космической инфляции. А во-вторых, непосредственная практическая польза от них для нужд и чаяний человечества несоизмеримо больше. Причем внятно объяснить, почему это так, вполне можно не только ученым специалистам, но и всем остальным людям, просто имеющим к данной теме интерес.
Ну а в качестве первого шага для начала объяснений вполне подойдет еще одно заметное событие из ленты текущих новостей. В первых числах сентября 2015 года мегакорпорация Intel объявила о начале 10-летнего сотрудничества с одним из знаменитых вузов Голландии, Делфтским университетом технологий, и с созданным при нем институтом квантовых исследований, QuTech.

Официальная цель взаимовыгодного сотрудничества – «ускорить прогресс в области квантовых вычислений».
Для достижения же этой цели Intel инвестирует в развитие проектов QuTech 50 миллионов долларов, попутно обязавшись предоставить свои «существенные инженерные ресурсы как в Делфте, так и в корпорации Intel, а также широкую техническую поддержку для исследований и разработок».
Дабы публика понимала, почему главный на этой планете производитель процессоров решил столь солидно вложиться в сугубо гипотетическую на сегодня область вычислительной техники, руководство Intel объяснило свое видение перспектив в отрасли примерно такими словами:
Что такое квантовые вычисления? В отличие от обычных цифровых компьютеров, которые работают на основе транзисторов, где данные закодированы в бинарных цифрах (битах), компьютеры квантовые используют особые квантовые биты (иначе именуемые кубитами). Эти кубиты могут существовать во множестве состояний одновременно, что предоставляет потенциал для проведения большого количества одновременных вычислений в параллели – существенно сокращая таким образом время отыскания ответа.
Поскольку далее нам понадобится несколько более глубокое представление о природе кубита как основы квантовых компьютеров, полезно сразу же выделить три принципиально важных аспекта в работе данного элемента.
Суть же достижений Делфтского технологического университета (привлекших к себе щедрую поддержку от Intel) как раз и заключается в том, что местным ученым удалось сконструировать такой кубит, который не только сам в высшей степени стабилен, но и способен формировать чрезвычайно устойчивые к помехам сцепленные состояния с другими такими же кубитами.
Причем построен этот новый кубит – что принципиально важно – на основе квазичастицы фермион Майораны. То есть того самого квантового объекта, который в физике твердого тела сначала выявили и теоретически описали Грег Мур и Ник Рид, а затем третий нынешний лауреат медали Дирака, Алексей Китаев, придумал на его основе «топологический квантовый компьютер» – совершенно новую концепцию квантового вычислителя, стойкого к искажениям и помехам окружающей среды.
Короче говоря, «все тут пошло от фермиона Майораны», а потому имеет смысл начинать историю именно с него.
⇡#Сюрпризы начинаются

Жизнь и творчество Этторе Майораны, гениального итальянского теоретика, бесследно и навсегда исчезнувшего в 1938 году, по сию пору остаются одной из самых загадочных страниц в истории науки на заре ядерной физики.
Другой великий физик-итальянец, нобелевский лауреат Энрико Ферми, близко знавший Майорану и хорошо представлявший масштаб его научного дарования, уверенно ставил этого ученого в один ряд с такими титанами, как Галилей, Ньютон или Эйнштейн. Однако человечество долгое время и понятия не имело, что за гиганта потеряла наука, когда этот странный и замкнутый молодой человек необъяснимо исчез с парома, шедшего из Палермо в Неаполь...
Многие десятилетия полного игнорирования работ Майораны понять довольно просто. Сам ученый безо всякого энтузиазма относился к оформлению своих научных открытий в виде статей (зачастую считая их тривиальными пустяками). А потому при жизни было опубликовано всего девять работ, написанных Майораной (причем почти все из них на итальянском языке, не самом, ясное дело, распространенном в научном сообществе).
К концу же XX века, когда масштаб прозрений этого гения, видевшего намного дальше и глубже современников, уже не вызывал никаких сомнений, в Италии сформировалась целая «небольшая индустрия» по исследованиям, анализам и интерпретациям всех тех блокнотов, черновиков и обрывочных записей, что остались после исчезновения Майораны.
Для нашей истории, однако, особый интерес представляет самая последняя из оформленных ученым статей, хотя и неохотно, но таки опубликованная им в 1937 году под сильнейшим нажимом со стороны Энрико Ферми. Именно в ней был найден и описан знаменитый ныне фермион Майораны – как одно из возможных решений весьма еще свежего по тем временам уравнения Дирака. То есть фундаментального уравнения квантовой механики, где в красивом, компактном и наиболее общем виде удалось соединить теорию относительности и волновую природу частиц со спином (то есть свойством собственного вращения).
Именно это уравнение одним из своих решений подтолкнуло Поля Дирака к теоретическому предсказанию античастиц материи. О существовании антиматерии никто прежде и понятия не имел, поэтому последовавшее вскоре экспериментальное открытие позитрона – как античастицы электрона – не только произвело на ученых сильнейшее впечатление, но и продемонстрировало подлинную мощь уравнения Дирака. Ну а Этторе Майорана сумел отыскать в той же математической структуре такое решение, которое выглядело совсем уж полным сюрпризом – оно описывало частицу, одновременно являющуюся и собственной античастицей.
Обычная физика взаимодействий для частицы и античастицы подразумевала лишь один вероятный исход – аннигиляцию, выброс энергии и взаимное уничтожение исходных частиц. Однако в фермионе Майораны получалось так, что частица и античастица могут, оказывается, вполне мирно сосуществовать друг с другом в состоянии суперпозиции. Но при этом – как следствие – демонстрируют весьма необычные свойства.
Когда одна и та же частица совмещает в себе характерные черты как положительно, так и отрицательно заряженного фермиона, это означает, что ее электрический заряд должен быть равным нулю. Аналогично оказываются равными нулю и прочие характеристики, отличавшие частицу от античастицы. Но в итоге это означает, что фермион Майораны вообще не имеет свойств, которые ученые могли бы измерить. Это делало гипотетическую частицу и чрезвычайно загадочной, и очень сложной для отыскания.
По собственному мнению первооткрывателя, фермион Майораны имел много общего с нейтрино – другой гипотетической и в высшей степени неуловимой частицей, предложенной чуть ранее Вольфгангом Паули для совсем иных целей. Но хотя сам факт изобильного существования нейтрино в космосе никаких сомнений в науке давно уже не вызывает, гигантские сложности в изучении этих частиц по сию пору так и не позволили уверенно подтвердить или опровергнуть их тождественность с фермионом Майораны.
С другой стороны, к концу XX века в физике появилась совершенно новая область исследований – под названием «квантовые вычисления». И во многом именно благодаря этому интерес к столь загадочному и неуловимому объекту, как фермион Майораны, возрос в чрезвычайной степени. Потому что главная «проблема» с данной частицей – её упорное ускользание от любых измерений – транcформировалась в её «замечательное качество». Ведь если у вас нет аппарата или инструмента, который мог бы измерить фермион Майораны, то это означает, что также вы и не можете его изменить...
Иначе говоря, высочайшая нечувствительность квантового объекта к внешним воздействиям делает его состояние очень надежным и устойчивым. А это – в случае освоения – сулит нам практически идеальный кубит для квантового компьютера. Проблема, по сути дела, лишь в том, чтобы найти настоящий фермион Майораны в природе... Или же, глядя на задачу несколько по-другому, попытаться сконструировать его самим. Благо и такой подход имеет полное право на существование.
⇡#Многоликие энионы
Сразу после окончания Второй мировой войны в истории квантовой физики случилось, к сожалению, разветвление на области высоких и низких энергий, из-за чего наука вполне определенно потеряла свою целостность.
Микромир квантовых частиц, как известно, можно изучать двумя главными способами. Либо сталкивая частицы в ускорителях, разгоняя их до все более и более высоких скоростей-энергий и повышая таким образом «разрешающую способность» столь специфического микроскопа, фиксирующего брызги столкновений. Либо же охлаждая подходящие материалы до сверхнизких температур, где помехи теплового шума минимальны, а квантовые эффекты приобретают макроскопический характер и уже поддаются прямым наблюдениям.
Оба направления исследований оказались в высшей степени успешными, а наработанная для них математика уравнений обладает совершенно выдающейся предсказательной мощью. Беда же в том, что для физики частиц высоких энергий математика работает одна, а для физики конденсированных сред при низких температурах – совсем другая. Более того, проникая все глубже в тайны строения микромира, на этих разных направлениях ученые постепенно сформировали и существенно различные представления о том, что они, собственно, исследуют.
В физике конденсированной материи с самого начала привыкли относиться к локальным возбуждениям среды как к «квазичастицам». Разного рода сгустки энергии в квантовом мире часто ведут себя как самостоятельные объекты (воздействуют на частицы и друг на друга, сами реагируют на внешние воздействия, волнами перемещаются в пространстве), а потому интерпретируются тоже как частицы и во множестве носят собственные отличительные имена — «дырки», магноны, фононы, экситоны и так далее.
В физике же высоких энергий все сложилось иначе. Поначалу гигантский зоопарк из самых разных «брызг-частиц» в космических излучениях и ускорителях постепенно удалось классифицировать и свести в куда более компактные классы «элементарных частиц» – типа кварков, глюонов или тяжелых бозонов. Эти объекты, надо подчеркнуть, куда логичнее было бы считать «квазичастицами», коль скоро они не существуют в природе сами по себе, как отдельные стабильные сущности вроде протона, электрона или фотона.
Но сугубо математические – поначалу – изобретения до того хорошо стали работать в качестве «частиц» в уравнениях, предсказывающих результаты опытов в ускорителях-коллайдерах, что их все чаще и чаще стали трактовать как «реальные» частицы. Так что на сегодняшний день кварки, глюоны и тяжелые бозоны – это все уже вроде как «факт природы». Абсолютно бесполезный, правда, для физики конденсированных сред...
Первые сигналы, указывающие на то, что у разных физик на самом деле таки должна иметься и общая математика, и общая концептуальная основа, начали поступать на рубеже 1970-80-х годов. Поначалу, правда, результаты эти выглядели просто как череда неожиданных открытий-сюрпризов в теоретических и экспериментальных областях, почти никак, на первый взгляд, друг с другом не связанных.

В области теории частиц сначала два никому не ведомых молодых норвежца, Лейнаас и Мюрхейм, а затем будущий нобелевский лауреат, американец Фрэнк Вильчек, работавший сам по себе, открыли весьма необычную «физику плоского мира». В привычном нам трехмерном пространстве все частицы природы по своим характерным свойствам распадаются на два существенно разных класса – фермионы с полуцелым спином (частицы материи типа электронов, протонов, нейтронов, имеющие спин ½) и бозоны с целочисленным спином (частицы излучения типа фотонов, имеющие спин 1, гипотетические гравитоны со спином 2 и так далее).
Когда же ученые решили математически исследовать природу частиц в двухмерном мире, то там, как оказалось, их поджидал большой сюрприз. В этих условиях частицы уже не расходятся столь же отчетливо по разным классам и порождают существенно иную физику взаимодействий – когда родовые различия между фермионами и бозонами размыты, поскольку вполне допустимы оказываются и дробные значения электрических зарядов, и произвольные дробные значения спинов. С подачи Фрэнка Вильчека такого рода гипотетические частицы стали называться «энионы» (anyons – от ANYthing, «что угодно»).
Случилось так, что в тот же самый период в области физики экспериментальной сначала был открыт квантовый эффект Холла (КЭХ), а спустя всего два года – еще и куда более неожиданный дробный квантовый эффект Холла (ДКЭХ). И по удивительному совпадению параллельное открытие энионов пришлось тут более чем кстати.
Собственно, эффект Холла был известен в физике еще с XIX века – как явление разделения электрических зарядов в проводнике под действием магнитного поля. Когда тот же эксперимент научились проводить в условиях сверхнизких температур и под действием более сильного магнитного поля, физика эффекта приобрела отчетливо квантовый характер, так что проводимость стала изменяться сугубо дискретными скачками, кратными значению заряда единичного электрона.
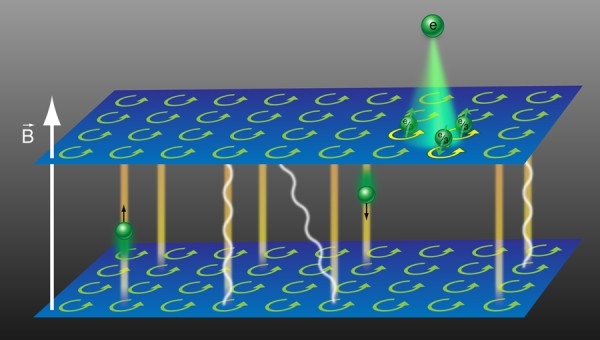
Ну а когда силу магнитного поля затем увеличили еще побольше, то получили сюрприз – в образце стали отмечаться признаки частиц проводимости с дробным электрическим зарядом. Поначалу – по аналогии с кварками в протоне – подумали было, что удалось обнаружить компоненты «неделимого электрона». Но проанализировав физику как следует, в итоге выяснили, что причиной стали особые вихри-квазичастицы в условиях двухмерной электронной жидкости.
Иначе говоря, было открыто коллективное поведение электронов, образующих в этой плоской жидкости такие вихревые образования, которые проявляют себя как частицы с дробным значением заряда. Причем, что интересно, уже в самых первых экспериментах с ДКЭХ значения зарядов у таких микровихрей-квазичастиц составляли 1/3 и 2/3 – в точности как у кварков, гипотетических частиц внутри протонов и нейтронов в физике высоких энергий.
Развивать эту аналогию, правда, теоретики не стали. Но зато вскоре было продемонстрировано, что экспериментально обнаруженные дробные квазичастицы в опытах с ДКЭХ – это и есть теоретические энионы Вильчека.
Ну а еще через несколько лет, в 1991-м, пара уже знакомых нам теоретиков, Мур и Рид (удостоенные ныне медали Дирака именно за это достижение), математически показали, что весьма особенный класс энионов – именуемых «неабелионы», или неабелевы энионы, – обладает набором таких характерных свойств, которые относят его к фермиону Майораны. В частности, именно в эту майорановскую категорию попадала и квазичастица-энион со спином 5/2, чуть ранее уже «вроде бы обнаруженная» в экспериментах «Лабораторий Белла» с кристаллами арсенида галлия (гигантские технические сложности при воспроизведении подобных опытов в других лабораториях по сию пору остаются главным тормозом развития)...
Это были весьма заметные и важные научные достижения, особенно для только-только нарождавшейся в ту пору области квантовых компьютеров. По свидетельству непосредственных участников процесса, в принципе, у многих тогда появилось интуитивное ощущение или предчувствие, если угодно, что именно здесь может быть потенциал для реального прорыва. Однако в какую-либо конкретную форму подобные смутные идеи поначалу не вырисовывались. Подлинные открытия начались с 1997 года – вместе с появлением работ Алексея Китаева о топологических квантовых вычислениях.
⇡#Топологические косы

Выпускник Физтеха в 1986-м, сотрудник Института теоретической физики им. Ландау до конца 1990-х и профессор Калтеха с начала 2000-х, Алексей Китаев всерьез заинтересовался квантовыми вычислениями в 1995-м. И как и все исследователи данной области, он очень быстро уперся в проблему чрезвычайной хрупкости квантовых состояний, моделируемых учеными в лабораториях. В качестве главного средства борьбы с этой бедой теоретики предлагали особые квантовые коды, исправляющие помехи и ошибки обработки. Однако для работы таких кодов требовалось в несколько раз увеличивать число сцепленных кубитов, а это само по себе — труднейшая в реализации задача...
Китаев же сумел посмотреть на проблему с существенно иной стороны, задавшись вполне естественным, в общем-то, вопросом: а как это может быть устроено в природе? Ведь понятно, что на самом нижнем уровне микромира частицы природы можно трактовать как базовые компоненты «натурального квантового компьютера» – то есть физической системы, которая не просто хранит и обрабатывает свои квантовые состояния, а делает это очень надежно.
Интуитивно несложно, наверное, понять, что в природных квантовых вычислениях не происходит ошибок по той причине, что природе каким-то хитрым образом удается изолировать обрабатываемую в ее квантовых системах информацию от воздействий среды и от ее помех. Куда сложнее постичь – как это сделал Китаев, что ключ к ответу на загадку могут давать топологические особенности, характерные для траекторий частиц в пространстве-времени...
Топология, можно напомнить, — это раздел математики о тех свойствах объекта, которые не меняются при его деформациях типа растяжения, сплющивания или изгибания. Иначе говоря, топологические свойства системы наиболее стабильны, а чтобы их разрушить, надо приложить к системе куда больше энергии, чем обычно. Так вот, Китаева осенило, что в природе квантовые вычисления состояний могут выполняться на топологических косах, которые сплетаются из нитей-траекторий, представляющих собой «мировые линии» движения частиц во времени и пространстве. Можно сказать, что длина такой нити изображает движение частицы во времени, а толщина косы – это физические размеры системы частиц в пространстве.

Иначе говоря, если в лабораториях ученых, экспериментирующих с кубитами, малейшие возмущения способны выбивать квантовые частицы в состояние декогеренции, внося бесконечные ошибки в вычисления, то для природных систем такого рода малые возмущения абсолютно никак не меняют топологические свойства кос. Ведь чтобы нарушить топологическую структуру косы, надо разорвать нити, приложив значительно большее усилие к системе. А потому в обычном диапазоне воздействий природная система всегда остается гибкой и стабильной...
Человеку, ясное дело, трудно тягаться с природой в оперировании «косами частиц во времени». Но самая грандиозная часть открытия Китаева заключалась в том, что одновременно он предложил и вполне практичный механизм для конструирования реального топологического компьютера – на основе очередного типа квазичастиц, неабелевых энионов. Практичным, правда, этот механизм является все еще лишь теоретически, поскольку из-за огромных технических трудностей о скором экспериментальном освоении такого рода объектов по-прежнему говорят весьма осторожно.
Но как бы там ни было, собственно идеи Китаева в мировом научном сообществе были приняты и по достоинству оценены практически сразу. В тот период времени неабелевы энионы и стойкий к ошибкам квантовый компьютинг существовали как две существенно разные темы. О вещах этих уже много чего было известно, и было понимание, что это интересно для разработок. Однако до Китаева никто не видел, насколько тесно две эти темы взаимосвязаны.
В чем же суть – совсем вкратце – топологически защищенных квантовых вычислений? В самом простом случае, когда в нашем мире вы меняете местами два идентичных предмета (две монетки на столе, к примеру), в описании этой системы ничего не меняется. В мире квантовом – когда вместо монеток оперируют частицами – перестановка пары обычных частиц, типа электронов, добавляет в математическое описание системы множитель «минус единица». Если же в качестве частиц выступают квазичастицы-энионы в плоском 2D-мире, то картина описания усложняется: множитель становится комплексным числом, а у характеристик оказываются несвойственные обычным частицам дробные значения.
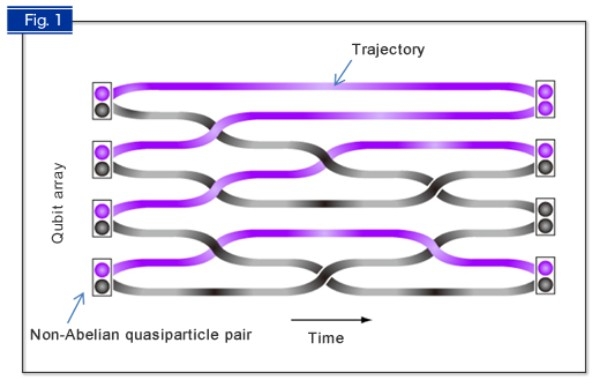
Ну а если, наконец, рассмотрение доходит до особого класса энионов, именуемых неабелевыми, то их простой обмен местами в системе отображается умножением уже не на число, а на матрицу. Главная же особенность множителя в виде матрицы в том, что это так называемая некоммутативная операция (иначе именуемая неабелевой). Другими словами, результат применения такой операции принципиально зависит от порядка следования элементов в описании. Конкретно для данного класса энионов это означает, что здесь оказывается существенным, в какую сторону крутят частицы при обмене их местами – по часовой стрелке или против. Ибо результирующее состояние в итоге оказывается существенно разным. То есть можно говорить, что здесь контролируемые человеком перестановки квазичастиц кодируют топологию заплетаемой косы системы во времени.
В итоге же получается, что система на неабелевых энионах по своей природе имеет именно такие правильные свойства, чтобы сделать возможными топологически защищенные от ошибок квантовые вычисления. Такая система несет в своих состояниях много информации, однако окружающая среда не может ни считывать, ни повреждать эту информацию – если смотреть на любую из частиц по одной за раз. Происходит же это по той причине, что здесь информация закодирована не в отдельных частицах, а в корне иначе – в весьма тонких и глубоких коллективных свойствах, разделяемых множеством частиц одновременно...
⇡#«Майорана» своими руками
Совершенно новое направление квантовых вычислений, открытое Китаевым, практически сразу начало получать мощное практическое воплощение. Уже в 1998 году с весьма необычной для нее инициативой выступила софтверная корпорация Microsoft, создав в Калифорнии для развития топологического квантового компьютинга специальный исследовательский центр Station Q, который возглавил известнейший математик-тополог, филдсовский медалист Майкл Фридман. А одним из первых научных сотрудников «Станции Кю» стал и россиянин Алексей Юрьевич Китаев (работал он там, правда, недолго, через несколько лет осев – теперь уже прочно – в Калифорнийском технологическом институте).

Но хотя поначалу перспективы быстрого прогресса на этом пути выглядели довольно радужно, череда экспериментальных неудач внесла в разработку темы свои суровые коррективы. Важные первичные успехи Боба Виллетта в Bell Labs с моделированием неабелевых энионов на полупроводниковых кристаллах арсенида галлия оказалось практически невозможно повторить в других лабораториях мира. О причинах этой неудачи разные эксперты говорят разное, но суть проблемы такова, что теоретикам пришлось активно подыскивать иные альтернативы.
И одну из наиболее интересных альтернатив – в сугубо теоретико-математическом виде – выдвинул опять-таки Алексей Китаев на рубеже 2000-2001 годов. На этот раз в его статье была представлена идея о переводе квантовых топологических вычислений из 2D-плоскости в еще более ограниченное 1D-пространство. Говоря конкретнее, расчеты Китаева продемонстрировали возможности для реализации фермиона Майораны в условиях абстрактной «одномерной решетки».
В переводе же на язык конкретной физической реализации такие вещи обычно означают весьма особые нанопроволочки, которые в условиях квантовой физики (при сверхнизком охлаждении и в сильном магнитном поле) начинают демонстрировать свойства одномерной квантовой системы. А поскольку нынешний бум нанотехнологий и активных проектов вокруг всевозможных наноматериалов породил множество продвинутых лабораторий такого рода по всему миру, и эта идея Китаева быстро нашла поддержку как у теоретиков, так и у экспериментаторов.
Самых же выдающихся и убедительных успехов с моделированием одномерного фермиона Майораны добился уже известный нам Делфтский технологический университет. О достижениях которого пора рассказать поподробнее.
Главой группы, добившейся в Делфте столь замечательных результатов, является профессор физики Лео Коувенховен (Leo Kouwenhoven), с именем которого по устоявшейся практике и связывают обычно все успехи. Хотя на самом деле, конечно же, это в очень значительной степени итог коллективных усилий, формировавшихся на основе исследований нескольких аспирантов и сотрудников лаборатории профессора.

Один из таких исследователей, в частности, по собственной программе занимался особенностями физики полупроводниковой нанопроволоки, соединяющей сверхпроводники. А когда появились публикации теоретиков, предсказывающие, что именно в такой конфигурации на концах проволочки могут, в принципе, обнаружиться фермионы Майораны, Коувенховен с соратниками и решил вплотную заняться поисками этой неуловимой квазичастицы – благо подходящая установка уже имелась у них заранее. Уверенности в успехе столь нового дела, естественно, у физиков не было, однако приятный сюрприз — открытие — не заставил себя ждать.
Можно говорить, что здесь фермион Майораны получается из суперпозиции электрона и «дырки» – как отсутствия электрона проводимости. Причем суперпозиция эта образуется на границах соединения полупроводника и сверхпроводника следующим образом. Когда к полупроводниковой нанопроволочке прикладывают магнитное поле, то электроны начинают двигаться вдоль проволоки вперед и назад – создавая на границе материалов две особые точки, каждая из которых имитирует половину электрона. При этом можно считать, что одновременно с электроном – но в противофазе – туда-сюда прыгает и «дырка».
И когда «дырка» в своих осцилляциях проводит равное количество времени там и тут, на каждой из сторон границы, то тогда, в квантово-механическом смысле, это и есть суперпозиция ее существенно разных состояний. Если же такая конструкция стабильна, то мы имеем полные основания называть объект квантовой квазичастицей. И поскольку в данном случае суперпозиция объединяет в себе колебания состояний отрицательно заряженного электрона и положительной дырки, есть все основания считать этот объект фермионом Майораны.
А что самое важное, здесь мы имеем не эфемерную неуловимую «Майорану», которая проявилась всего лишь на миг и тут же навсегда исчезла. Напротив, здесь человек может удерживать частицу стабильно и смотреть на нее столько, сколько захочется. Точнее, столько, сколько требуется кубитам для выполнения алгоритмов квантовых вычислений.

На сегодняшний день, в частности, время удержания фермиона Майораны в Делфте исчисляется уже минутами. Для работы квантового компьютера этого обычно вполне достаточно. Так что делфтскому институту QuTech для закрепления успеха осталось сконструировать из своей квазичастицы практичный топологический кубит и обеспечить таким кубитам квантовую сцепленность для формирования когерентной вычислительной системы.
Все это, ясное дело, в высшей степени непростые технологические проблемы. Но для решения именно этих задач на подмогу к QuTech и пришла ныне корпорация-гигант Intel – со своими ресурсами, инженерами и инвестициями в размере 50 миллионов долларов. Так что все тут, практически наверняка, должно склеиться.
⇡#Намного больше, чем просто сюрпризы
Любой обзорный рассказ о прогрессе топологических квантовых компьютеров окажется заведомо неполным, если не упомянуть – хотя бы в нескольких фразах – и один чрезвычайно важный аспект в нынешней картине развития фундаментальной теоретической физики. Ибо аспект этот напрямую связывает успехи очевидно прикладных задач квантовых вычислений и сугубо теоретические – почти метафизические – изыскания науки относительно наиболее глубоких и загадочных механизмов в основе устройства природы.
Ибо чем дальше, тем больше получают теоретики такие свидетельства, которые совершенно определенно указывают на основополагающую роль информации в основе работы всей квантовой физики. Первые сигналы о начале постижения этой важнейшей взаимосвязи стали поступать еще на заре 1990-х годов – когда патриарх теоретической физики Джон Уилер (отец термина «черные дыры») впервые изрек свою афористичную формулу It from bit, то есть «Все в этом мире из битов».
Поначалу, естественно, очень многие не восприняли Уилера всерьез, особенно исследователи в области частиц высоких энергий, со времен создания атомной бомбы привыкшие считать именно себя наиболее передовым авангардом физики. Но время шло, содержательные результаты нарабатывались, и постепенно все больше и больше ученых убеждалось, сколь плодотворно и гармонично квантовая физика и теория информации дополняют друг друга – словно это разные стороны одного и того же.
И случилось так, что при подобных раскладах квантовые компьютеры и лежащий в их основе феномен квантовой сцепленности все чаще и чаще стали оказываться в фокусе междисциплинарных изысканий, которые неожиданно для всех обнаруживают глубинное единство природы в эквивалентности математических описаний для совершенно разных, казалось бы, вещей.

В эквивалентности таких, скажем, объектов, как черные дыры Вселенной (частицы макрокосмоса) и элементарные частицы материи (черные дыры микромира). В эквивалентности сильных ядерных взаимодействий в глубинах атома и слабых гравитационных взаимодействий на гигантских расстояниях космоса. В эквивалентности сугубо квантового феномена ЭПР (мгновенное взаимодействие сцепленных частиц на любых расстояниях) и межпространственного космического туннеля, «моста ЭР», связывающего сколь угодно разнесенные концы вселенной...
Все эти открытия происходили в фундаментальной науке постепенно, и уже должны были, казалось бы, приучить сообщество к тому, что сами основы современной физики ныне существенно изменяются. Тем не менее для очень многих стало большим сюрпризом, когда осенью 2015 года Джон Прескилл, известнейший специалист по квантовой информатике, опубликовал такой вот график – с динамикой публикаций тех научных статей по физике высоких энергий, которые содержат в своем названии термин Entanglement, то есть «квантовая сцепленность».
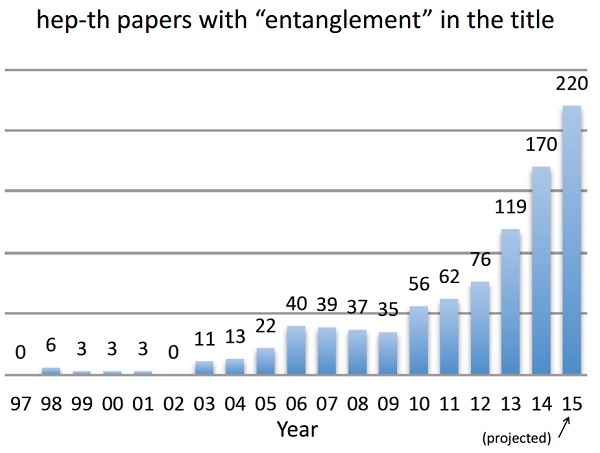
Для того, чтобы и неспециалистам стала понятна поразительная суть этой диаграммы, демонстрирующей стремительный взлет темы Entanglement, достаточно лишь пояснить, что на протяжении всего XX века очень тонкий (и для многих в ту пору крайне сомнительный) феномен квантовой сцепленности в физике высоких энергий не фигурировал вообще никак. Да и сегодня, в общем-то, к экспериментам с ускорителями-коллайдерами эта тема никакого отношения не имеет.
И тем не менее стремительный рост статей об Entanglement именно в этой секции библиотеки препринтов Arxiv.org наглядно свидетельствует о том, что и здесь теоретики всерьез занялись изучением квантово-информационных аспектов своей науки. Ну а разработчики квантовых компьютеров, в свою очередь, понемногу начинают обнаруживать, что как бы «придуманные ими самими» технические хитрости – вроде неабелевых энионов плоского 2D-мира – в других областях исследований выявляются на фундаментальных, «самых нижних» уровнях устройства природы...
В частности, сейчас имеются по меньшей мере три существенно разных разработки (от весьма известных в физике людей), указывающих на то, что при мельчайших масштабах уровня планковских длин (10-35 м) наше пространство имеет размерность 2. А затем, по мере нарастания масштаба, размерность быстро нарастает до привычных всем четырех измерений пространства-времени.
Более того, в смежной области исследований получены столь же интересные результаты (от «отца энионов» Фрэнка Вильчека), описывающие конкретный математический механизм для порождения в природе настоящих «кос», вытягивающихся за системами частиц в квантовом мнимом времени – как их материальная «мировая линия»... И есть интересные свидетельства тому, что это не только квантовая память частиц природы, но и одновременно основа Mind-Stuff – то есть «материи разума» Вселенной, пользуясь известным термином от Уильяма Кингдона Клиффорда.
Но это все, конечно же, отдельная тема для совсем другого большого рассказа.
04 ноября 2015 Бёрд Киви
Топологический квантовый компьютер пока что никто сделать не сумел. Но суть идей в основе этой концепции необычайно красива, а практические успехи на пути её освоения уже несомненны. Так что в итоге наверняка все должно получиться
Сюрпризы начинаются
В принципе, данный материал вполне можно было бы озаглавить «Другая физика». Потому что весь набор результатов, получаемых в процессе освоения области с громким названием «топологические квантовые вычисления» – это, по сути дела, тихая, незаметная и одновременно великая научная революция.

Если приглядеться, то в данном направлении буквально каждый шаг – от истории зарождения и вплоть до новейших достижений – хотя бы чуть-чуть (а порою существенно) изменяет и переворачивает устоявшиеся научные представления об устройстве окружающего мира. Но поскольку происходит это все очень постепенно, никто как бы не замечает, что вся физика тоже попутно переворачивается — с головы на ноги.
Ну а чтобы столь важный процесс стал не только заметным, но и вполне понятным, рассказывать историю надо в общей исторической ретроспективе. Однако начать лучше все же с самых последних новостей – для общего представления о ситуации в столь интересной области и о масштабе происходящих перемен.
Пять тысяч и 50 миллионов
Ежегодно 8 августа – в день рождения П. А. М. Дирака – мировая наука отмечает наиболее выдающиеся достижения в сфере теоретической физики. По давно заведенной традиции, лауреатов очередной Медали Дирака принято выбирать среди тех теоретиков, которым еще не довелось получить Нобелевскую премию. И хотя сопутствующий денежный приз совсем невелик, всего 5 тысяч евро, медаль Дирака считается в физическом сообществе весьма престижной и почетной наградой.

Чаще всего этот приз достается исследователям, занимающимся либо физикой частиц высоких энергий и теорией струн, либо космологией и теорией инфляции (считается, что именно там проходят передовые рубежи физической науки). Однако в нынешнем году медалью Дирака было решено наградить трех ученых, известных по своим работам в области физики конденсированных сред, – Алексея Китаева, Грегори Мура и Николаса Рида. Как сказано в официальном представлении к награде, «за их междисциплинарные вклады, обеспечившие введение концепций конформной теории поля и статистики неабелевых квазичастиц в системы конденсированной материи и применение этих идей к квантовым вычислениям. Работы этих ученых сыграли фундаментальную роль для последних успехов в нашем понимании квантовых состояний материи и квантовой сцепленности. А также породили интенсивный экспериментальный поиск квазичастиц Майораны – возбуждений материи, действующих как своя собственная античастица...»
Для обычных людей, далеких от высоких сфер теоретической физики и не владеющих профессиональной терминологией, подобные разъяснения не объясняют практически ничего. К великому сожалению. Потому что на самом деле речь тут идет о вещах, которые, во-первых, ничуть не менее важны для науки, чем Большой адронный коллайдер или теория космической инфляции. А во-вторых, непосредственная практическая польза от них для нужд и чаяний человечества несоизмеримо больше. Причем внятно объяснить, почему это так, вполне можно не только ученым специалистам, но и всем остальным людям, просто имеющим к данной теме интерес.
Ну а в качестве первого шага для начала объяснений вполне подойдет еще одно заметное событие из ленты текущих новостей. В первых числах сентября 2015 года мегакорпорация Intel объявила о начале 10-летнего сотрудничества с одним из знаменитых вузов Голландии, Делфтским университетом технологий, и с созданным при нем институтом квантовых исследований, QuTech.

Официальная цель взаимовыгодного сотрудничества – «ускорить прогресс в области квантовых вычислений».
Для достижения же этой цели Intel инвестирует в развитие проектов QuTech 50 миллионов долларов, попутно обязавшись предоставить свои «существенные инженерные ресурсы как в Делфте, так и в корпорации Intel, а также широкую техническую поддержку для исследований и разработок».
Дабы публика понимала, почему главный на этой планете производитель процессоров решил столь солидно вложиться в сугубо гипотетическую на сегодня область вычислительной техники, руководство Intel объяснило свое видение перспектив в отрасли примерно такими словами:
Что такое квантовые вычисления? В отличие от обычных цифровых компьютеров, которые работают на основе транзисторов, где данные закодированы в бинарных цифрах (битах), компьютеры квантовые используют особые квантовые биты (иначе именуемые кубитами). Эти кубиты могут существовать во множестве состояний одновременно, что предоставляет потенциал для проведения большого количества одновременных вычислений в параллели – существенно сокращая таким образом время отыскания ответа.
Поскольку далее нам понадобится несколько более глубокое представление о природе кубита как основы квантовых компьютеров, полезно сразу же выделить три принципиально важных аспекта в работе данного элемента.
- Суперпозиция состояний. Как всякий объект квантового мира, кубит имеет волновую природу, то есть постоянные изменения его состояний описываются волновой функцией. И если максимум волны описывать как 1, а минимум как 0, то кубит постоянно – но с разными вероятностями – пребывает и в этих крайних, и во всех промежуточных состояниях волны (именуемых фазами).
- Интерференция кубитов. Как и повсюду в волновой физике, при взаимодействии множества волн от разных источников порождается интерференционная картина. Согласовывая фазы источников волн, такие картины – или паттерны – можно делать устойчивыми, а в квантовом компьютере именно такой паттерн заранее известного нужного вида сигнализирует о получении ответа для вычислительной задачи. Зафиксированные в этот момент фазовые состояния кубитов (единицы и нули) с высокой вероятностью кодируют в себе искомый ответ. Суть же алгоритмов для квантовых вычислений в том, чтобы тонкими неразрушающими воздействиями на кубиты выводить их совместно согласованные осцилляции к порождению нужной интерференционной картины.

- Сцепленность кубитов. Для того чтобы суперпозиции множества кубитов в квантовом компьютере вели себя как единая согласованная система, именуемая когерентной, кубиты должны находиться в состоянии квантовой сцепленности друг с другом. Это сугубо квантовое свойство частиц микромира, благодаря которому измерение (разрушающее изменение) состояния хотя бы одного кубита приводит к мгновенному изменению (фиксации) состояний и всех остальных кубитов системы. Именно так квантовый компьютер «выходит» на нужный ответ, но также именно здесь сосредоточена и гигантская проблема в освоении столь заманчивой технологии.
Суть же достижений Делфтского технологического университета (привлекших к себе щедрую поддержку от Intel) как раз и заключается в том, что местным ученым удалось сконструировать такой кубит, который не только сам в высшей степени стабилен, но и способен формировать чрезвычайно устойчивые к помехам сцепленные состояния с другими такими же кубитами.
Причем построен этот новый кубит – что принципиально важно – на основе квазичастицы фермион Майораны. То есть того самого квантового объекта, который в физике твердого тела сначала выявили и теоретически описали Грег Мур и Ник Рид, а затем третий нынешний лауреат медали Дирака, Алексей Китаев, придумал на его основе «топологический квантовый компьютер» – совершенно новую концепцию квантового вычислителя, стойкого к искажениям и помехам окружающей среды.
Короче говоря, «все тут пошло от фермиона Майораны», а потому имеет смысл начинать историю именно с него.
⇡#Сюрпризы начинаются

Жизнь и творчество Этторе Майораны, гениального итальянского теоретика, бесследно и навсегда исчезнувшего в 1938 году, по сию пору остаются одной из самых загадочных страниц в истории науки на заре ядерной физики.
Другой великий физик-итальянец, нобелевский лауреат Энрико Ферми, близко знавший Майорану и хорошо представлявший масштаб его научного дарования, уверенно ставил этого ученого в один ряд с такими титанами, как Галилей, Ньютон или Эйнштейн. Однако человечество долгое время и понятия не имело, что за гиганта потеряла наука, когда этот странный и замкнутый молодой человек необъяснимо исчез с парома, шедшего из Палермо в Неаполь...
Многие десятилетия полного игнорирования работ Майораны понять довольно просто. Сам ученый безо всякого энтузиазма относился к оформлению своих научных открытий в виде статей (зачастую считая их тривиальными пустяками). А потому при жизни было опубликовано всего девять работ, написанных Майораной (причем почти все из них на итальянском языке, не самом, ясное дело, распространенном в научном сообществе).
К концу же XX века, когда масштаб прозрений этого гения, видевшего намного дальше и глубже современников, уже не вызывал никаких сомнений, в Италии сформировалась целая «небольшая индустрия» по исследованиям, анализам и интерпретациям всех тех блокнотов, черновиков и обрывочных записей, что остались после исчезновения Майораны.
Для нашей истории, однако, особый интерес представляет самая последняя из оформленных ученым статей, хотя и неохотно, но таки опубликованная им в 1937 году под сильнейшим нажимом со стороны Энрико Ферми. Именно в ней был найден и описан знаменитый ныне фермион Майораны – как одно из возможных решений весьма еще свежего по тем временам уравнения Дирака. То есть фундаментального уравнения квантовой механики, где в красивом, компактном и наиболее общем виде удалось соединить теорию относительности и волновую природу частиц со спином (то есть свойством собственного вращения).

Именно это уравнение одним из своих решений подтолкнуло Поля Дирака к теоретическому предсказанию античастиц материи. О существовании антиматерии никто прежде и понятия не имел, поэтому последовавшее вскоре экспериментальное открытие позитрона – как античастицы электрона – не только произвело на ученых сильнейшее впечатление, но и продемонстрировало подлинную мощь уравнения Дирака. Ну а Этторе Майорана сумел отыскать в той же математической структуре такое решение, которое выглядело совсем уж полным сюрпризом – оно описывало частицу, одновременно являющуюся и собственной античастицей.
Обычная физика взаимодействий для частицы и античастицы подразумевала лишь один вероятный исход – аннигиляцию, выброс энергии и взаимное уничтожение исходных частиц. Однако в фермионе Майораны получалось так, что частица и античастица могут, оказывается, вполне мирно сосуществовать друг с другом в состоянии суперпозиции. Но при этом – как следствие – демонстрируют весьма необычные свойства.
Когда одна и та же частица совмещает в себе характерные черты как положительно, так и отрицательно заряженного фермиона, это означает, что ее электрический заряд должен быть равным нулю. Аналогично оказываются равными нулю и прочие характеристики, отличавшие частицу от античастицы. Но в итоге это означает, что фермион Майораны вообще не имеет свойств, которые ученые могли бы измерить. Это делало гипотетическую частицу и чрезвычайно загадочной, и очень сложной для отыскания.
По собственному мнению первооткрывателя, фермион Майораны имел много общего с нейтрино – другой гипотетической и в высшей степени неуловимой частицей, предложенной чуть ранее Вольфгангом Паули для совсем иных целей. Но хотя сам факт изобильного существования нейтрино в космосе никаких сомнений в науке давно уже не вызывает, гигантские сложности в изучении этих частиц по сию пору так и не позволили уверенно подтвердить или опровергнуть их тождественность с фермионом Майораны.

С другой стороны, к концу XX века в физике появилась совершенно новая область исследований – под названием «квантовые вычисления». И во многом именно благодаря этому интерес к столь загадочному и неуловимому объекту, как фермион Майораны, возрос в чрезвычайной степени. Потому что главная «проблема» с данной частицей – её упорное ускользание от любых измерений – транcформировалась в её «замечательное качество». Ведь если у вас нет аппарата или инструмента, который мог бы измерить фермион Майораны, то это означает, что также вы и не можете его изменить...
Иначе говоря, высочайшая нечувствительность квантового объекта к внешним воздействиям делает его состояние очень надежным и устойчивым. А это – в случае освоения – сулит нам практически идеальный кубит для квантового компьютера. Проблема, по сути дела, лишь в том, чтобы найти настоящий фермион Майораны в природе... Или же, глядя на задачу несколько по-другому, попытаться сконструировать его самим. Благо и такой подход имеет полное право на существование.
⇡#Многоликие энионы
Сразу после окончания Второй мировой войны в истории квантовой физики случилось, к сожалению, разветвление на области высоких и низких энергий, из-за чего наука вполне определенно потеряла свою целостность.
Микромир квантовых частиц, как известно, можно изучать двумя главными способами. Либо сталкивая частицы в ускорителях, разгоняя их до все более и более высоких скоростей-энергий и повышая таким образом «разрешающую способность» столь специфического микроскопа, фиксирующего брызги столкновений. Либо же охлаждая подходящие материалы до сверхнизких температур, где помехи теплового шума минимальны, а квантовые эффекты приобретают макроскопический характер и уже поддаются прямым наблюдениям.
Оба направления исследований оказались в высшей степени успешными, а наработанная для них математика уравнений обладает совершенно выдающейся предсказательной мощью. Беда же в том, что для физики частиц высоких энергий математика работает одна, а для физики конденсированных сред при низких температурах – совсем другая. Более того, проникая все глубже в тайны строения микромира, на этих разных направлениях ученые постепенно сформировали и существенно различные представления о том, что они, собственно, исследуют.

В физике конденсированной материи с самого начала привыкли относиться к локальным возбуждениям среды как к «квазичастицам». Разного рода сгустки энергии в квантовом мире часто ведут себя как самостоятельные объекты (воздействуют на частицы и друг на друга, сами реагируют на внешние воздействия, волнами перемещаются в пространстве), а потому интерпретируются тоже как частицы и во множестве носят собственные отличительные имена — «дырки», магноны, фононы, экситоны и так далее.
В физике же высоких энергий все сложилось иначе. Поначалу гигантский зоопарк из самых разных «брызг-частиц» в космических излучениях и ускорителях постепенно удалось классифицировать и свести в куда более компактные классы «элементарных частиц» – типа кварков, глюонов или тяжелых бозонов. Эти объекты, надо подчеркнуть, куда логичнее было бы считать «квазичастицами», коль скоро они не существуют в природе сами по себе, как отдельные стабильные сущности вроде протона, электрона или фотона.
Но сугубо математические – поначалу – изобретения до того хорошо стали работать в качестве «частиц» в уравнениях, предсказывающих результаты опытов в ускорителях-коллайдерах, что их все чаще и чаще стали трактовать как «реальные» частицы. Так что на сегодняшний день кварки, глюоны и тяжелые бозоны – это все уже вроде как «факт природы». Абсолютно бесполезный, правда, для физики конденсированных сред...
Первые сигналы, указывающие на то, что у разных физик на самом деле таки должна иметься и общая математика, и общая концептуальная основа, начали поступать на рубеже 1970-80-х годов. Поначалу, правда, результаты эти выглядели просто как череда неожиданных открытий-сюрпризов в теоретических и экспериментальных областях, почти никак, на первый взгляд, друг с другом не связанных.

В области теории частиц сначала два никому не ведомых молодых норвежца, Лейнаас и Мюрхейм, а затем будущий нобелевский лауреат, американец Фрэнк Вильчек, работавший сам по себе, открыли весьма необычную «физику плоского мира». В привычном нам трехмерном пространстве все частицы природы по своим характерным свойствам распадаются на два существенно разных класса – фермионы с полуцелым спином (частицы материи типа электронов, протонов, нейтронов, имеющие спин ½) и бозоны с целочисленным спином (частицы излучения типа фотонов, имеющие спин 1, гипотетические гравитоны со спином 2 и так далее).
Когда же ученые решили математически исследовать природу частиц в двухмерном мире, то там, как оказалось, их поджидал большой сюрприз. В этих условиях частицы уже не расходятся столь же отчетливо по разным классам и порождают существенно иную физику взаимодействий – когда родовые различия между фермионами и бозонами размыты, поскольку вполне допустимы оказываются и дробные значения электрических зарядов, и произвольные дробные значения спинов. С подачи Фрэнка Вильчека такого рода гипотетические частицы стали называться «энионы» (anyons – от ANYthing, «что угодно»).
Случилось так, что в тот же самый период в области физики экспериментальной сначала был открыт квантовый эффект Холла (КЭХ), а спустя всего два года – еще и куда более неожиданный дробный квантовый эффект Холла (ДКЭХ). И по удивительному совпадению параллельное открытие энионов пришлось тут более чем кстати.
Собственно, эффект Холла был известен в физике еще с XIX века – как явление разделения электрических зарядов в проводнике под действием магнитного поля. Когда тот же эксперимент научились проводить в условиях сверхнизких температур и под действием более сильного магнитного поля, физика эффекта приобрела отчетливо квантовый характер, так что проводимость стала изменяться сугубо дискретными скачками, кратными значению заряда единичного электрона.

Ну а когда силу магнитного поля затем увеличили еще побольше, то получили сюрприз – в образце стали отмечаться признаки частиц проводимости с дробным электрическим зарядом. Поначалу – по аналогии с кварками в протоне – подумали было, что удалось обнаружить компоненты «неделимого электрона». Но проанализировав физику как следует, в итоге выяснили, что причиной стали особые вихри-квазичастицы в условиях двухмерной электронной жидкости.
Иначе говоря, было открыто коллективное поведение электронов, образующих в этой плоской жидкости такие вихревые образования, которые проявляют себя как частицы с дробным значением заряда. Причем, что интересно, уже в самых первых экспериментах с ДКЭХ значения зарядов у таких микровихрей-квазичастиц составляли 1/3 и 2/3 – в точности как у кварков, гипотетических частиц внутри протонов и нейтронов в физике высоких энергий.
Развивать эту аналогию, правда, теоретики не стали. Но зато вскоре было продемонстрировано, что экспериментально обнаруженные дробные квазичастицы в опытах с ДКЭХ – это и есть теоретические энионы Вильчека.
Ну а еще через несколько лет, в 1991-м, пара уже знакомых нам теоретиков, Мур и Рид (удостоенные ныне медали Дирака именно за это достижение), математически показали, что весьма особенный класс энионов – именуемых «неабелионы», или неабелевы энионы, – обладает набором таких характерных свойств, которые относят его к фермиону Майораны. В частности, именно в эту майорановскую категорию попадала и квазичастица-энион со спином 5/2, чуть ранее уже «вроде бы обнаруженная» в экспериментах «Лабораторий Белла» с кристаллами арсенида галлия (гигантские технические сложности при воспроизведении подобных опытов в других лабораториях по сию пору остаются главным тормозом развития)...
Это были весьма заметные и важные научные достижения, особенно для только-только нарождавшейся в ту пору области квантовых компьютеров. По свидетельству непосредственных участников процесса, в принципе, у многих тогда появилось интуитивное ощущение или предчувствие, если угодно, что именно здесь может быть потенциал для реального прорыва. Однако в какую-либо конкретную форму подобные смутные идеи поначалу не вырисовывались. Подлинные открытия начались с 1997 года – вместе с появлением работ Алексея Китаева о топологических квантовых вычислениях.
⇡#Топологические косы

Выпускник Физтеха в 1986-м, сотрудник Института теоретической физики им. Ландау до конца 1990-х и профессор Калтеха с начала 2000-х, Алексей Китаев всерьез заинтересовался квантовыми вычислениями в 1995-м. И как и все исследователи данной области, он очень быстро уперся в проблему чрезвычайной хрупкости квантовых состояний, моделируемых учеными в лабораториях. В качестве главного средства борьбы с этой бедой теоретики предлагали особые квантовые коды, исправляющие помехи и ошибки обработки. Однако для работы таких кодов требовалось в несколько раз увеличивать число сцепленных кубитов, а это само по себе — труднейшая в реализации задача...
Китаев же сумел посмотреть на проблему с существенно иной стороны, задавшись вполне естественным, в общем-то, вопросом: а как это может быть устроено в природе? Ведь понятно, что на самом нижнем уровне микромира частицы природы можно трактовать как базовые компоненты «натурального квантового компьютера» – то есть физической системы, которая не просто хранит и обрабатывает свои квантовые состояния, а делает это очень надежно.
Интуитивно несложно, наверное, понять, что в природных квантовых вычислениях не происходит ошибок по той причине, что природе каким-то хитрым образом удается изолировать обрабатываемую в ее квантовых системах информацию от воздействий среды и от ее помех. Куда сложнее постичь – как это сделал Китаев, что ключ к ответу на загадку могут давать топологические особенности, характерные для траекторий частиц в пространстве-времени...
Топология, можно напомнить, — это раздел математики о тех свойствах объекта, которые не меняются при его деформациях типа растяжения, сплющивания или изгибания. Иначе говоря, топологические свойства системы наиболее стабильны, а чтобы их разрушить, надо приложить к системе куда больше энергии, чем обычно. Так вот, Китаева осенило, что в природе квантовые вычисления состояний могут выполняться на топологических косах, которые сплетаются из нитей-траекторий, представляющих собой «мировые линии» движения частиц во времени и пространстве. Можно сказать, что длина такой нити изображает движение частицы во времени, а толщина косы – это физические размеры системы частиц в пространстве.

Иначе говоря, если в лабораториях ученых, экспериментирующих с кубитами, малейшие возмущения способны выбивать квантовые частицы в состояние декогеренции, внося бесконечные ошибки в вычисления, то для природных систем такого рода малые возмущения абсолютно никак не меняют топологические свойства кос. Ведь чтобы нарушить топологическую структуру косы, надо разорвать нити, приложив значительно большее усилие к системе. А потому в обычном диапазоне воздействий природная система всегда остается гибкой и стабильной...
Человеку, ясное дело, трудно тягаться с природой в оперировании «косами частиц во времени». Но самая грандиозная часть открытия Китаева заключалась в том, что одновременно он предложил и вполне практичный механизм для конструирования реального топологического компьютера – на основе очередного типа квазичастиц, неабелевых энионов. Практичным, правда, этот механизм является все еще лишь теоретически, поскольку из-за огромных технических трудностей о скором экспериментальном освоении такого рода объектов по-прежнему говорят весьма осторожно.
Но как бы там ни было, собственно идеи Китаева в мировом научном сообществе были приняты и по достоинству оценены практически сразу. В тот период времени неабелевы энионы и стойкий к ошибкам квантовый компьютинг существовали как две существенно разные темы. О вещах этих уже много чего было известно, и было понимание, что это интересно для разработок. Однако до Китаева никто не видел, насколько тесно две эти темы взаимосвязаны.
В чем же суть – совсем вкратце – топологически защищенных квантовых вычислений? В самом простом случае, когда в нашем мире вы меняете местами два идентичных предмета (две монетки на столе, к примеру), в описании этой системы ничего не меняется. В мире квантовом – когда вместо монеток оперируют частицами – перестановка пары обычных частиц, типа электронов, добавляет в математическое описание системы множитель «минус единица». Если же в качестве частиц выступают квазичастицы-энионы в плоском 2D-мире, то картина описания усложняется: множитель становится комплексным числом, а у характеристик оказываются несвойственные обычным частицам дробные значения.

Ну а если, наконец, рассмотрение доходит до особого класса энионов, именуемых неабелевыми, то их простой обмен местами в системе отображается умножением уже не на число, а на матрицу. Главная же особенность множителя в виде матрицы в том, что это так называемая некоммутативная операция (иначе именуемая неабелевой). Другими словами, результат применения такой операции принципиально зависит от порядка следования элементов в описании. Конкретно для данного класса энионов это означает, что здесь оказывается существенным, в какую сторону крутят частицы при обмене их местами – по часовой стрелке или против. Ибо результирующее состояние в итоге оказывается существенно разным. То есть можно говорить, что здесь контролируемые человеком перестановки квазичастиц кодируют топологию заплетаемой косы системы во времени.
В итоге же получается, что система на неабелевых энионах по своей природе имеет именно такие правильные свойства, чтобы сделать возможными топологически защищенные от ошибок квантовые вычисления. Такая система несет в своих состояниях много информации, однако окружающая среда не может ни считывать, ни повреждать эту информацию – если смотреть на любую из частиц по одной за раз. Происходит же это по той причине, что здесь информация закодирована не в отдельных частицах, а в корне иначе – в весьма тонких и глубоких коллективных свойствах, разделяемых множеством частиц одновременно...
⇡#«Майорана» своими руками
Совершенно новое направление квантовых вычислений, открытое Китаевым, практически сразу начало получать мощное практическое воплощение. Уже в 1998 году с весьма необычной для нее инициативой выступила софтверная корпорация Microsoft, создав в Калифорнии для развития топологического квантового компьютинга специальный исследовательский центр Station Q, который возглавил известнейший математик-тополог, филдсовский медалист Майкл Фридман. А одним из первых научных сотрудников «Станции Кю» стал и россиянин Алексей Юрьевич Китаев (работал он там, правда, недолго, через несколько лет осев – теперь уже прочно – в Калифорнийском технологическом институте).

Но хотя поначалу перспективы быстрого прогресса на этом пути выглядели довольно радужно, череда экспериментальных неудач внесла в разработку темы свои суровые коррективы. Важные первичные успехи Боба Виллетта в Bell Labs с моделированием неабелевых энионов на полупроводниковых кристаллах арсенида галлия оказалось практически невозможно повторить в других лабораториях мира. О причинах этой неудачи разные эксперты говорят разное, но суть проблемы такова, что теоретикам пришлось активно подыскивать иные альтернативы.
И одну из наиболее интересных альтернатив – в сугубо теоретико-математическом виде – выдвинул опять-таки Алексей Китаев на рубеже 2000-2001 годов. На этот раз в его статье была представлена идея о переводе квантовых топологических вычислений из 2D-плоскости в еще более ограниченное 1D-пространство. Говоря конкретнее, расчеты Китаева продемонстрировали возможности для реализации фермиона Майораны в условиях абстрактной «одномерной решетки».
В переводе же на язык конкретной физической реализации такие вещи обычно означают весьма особые нанопроволочки, которые в условиях квантовой физики (при сверхнизком охлаждении и в сильном магнитном поле) начинают демонстрировать свойства одномерной квантовой системы. А поскольку нынешний бум нанотехнологий и активных проектов вокруг всевозможных наноматериалов породил множество продвинутых лабораторий такого рода по всему миру, и эта идея Китаева быстро нашла поддержку как у теоретиков, так и у экспериментаторов.
Самых же выдающихся и убедительных успехов с моделированием одномерного фермиона Майораны добился уже известный нам Делфтский технологический университет. О достижениях которого пора рассказать поподробнее.
Главой группы, добившейся в Делфте столь замечательных результатов, является профессор физики Лео Коувенховен (Leo Kouwenhoven), с именем которого по устоявшейся практике и связывают обычно все успехи. Хотя на самом деле, конечно же, это в очень значительной степени итог коллективных усилий, формировавшихся на основе исследований нескольких аспирантов и сотрудников лаборатории профессора.

Один из таких исследователей, в частности, по собственной программе занимался особенностями физики полупроводниковой нанопроволоки, соединяющей сверхпроводники. А когда появились публикации теоретиков, предсказывающие, что именно в такой конфигурации на концах проволочки могут, в принципе, обнаружиться фермионы Майораны, Коувенховен с соратниками и решил вплотную заняться поисками этой неуловимой квазичастицы – благо подходящая установка уже имелась у них заранее. Уверенности в успехе столь нового дела, естественно, у физиков не было, однако приятный сюрприз — открытие — не заставил себя ждать.
Можно говорить, что здесь фермион Майораны получается из суперпозиции электрона и «дырки» – как отсутствия электрона проводимости. Причем суперпозиция эта образуется на границах соединения полупроводника и сверхпроводника следующим образом. Когда к полупроводниковой нанопроволочке прикладывают магнитное поле, то электроны начинают двигаться вдоль проволоки вперед и назад – создавая на границе материалов две особые точки, каждая из которых имитирует половину электрона. При этом можно считать, что одновременно с электроном – но в противофазе – туда-сюда прыгает и «дырка».
И когда «дырка» в своих осцилляциях проводит равное количество времени там и тут, на каждой из сторон границы, то тогда, в квантово-механическом смысле, это и есть суперпозиция ее существенно разных состояний. Если же такая конструкция стабильна, то мы имеем полные основания называть объект квантовой квазичастицей. И поскольку в данном случае суперпозиция объединяет в себе колебания состояний отрицательно заряженного электрона и положительной дырки, есть все основания считать этот объект фермионом Майораны.
А что самое важное, здесь мы имеем не эфемерную неуловимую «Майорану», которая проявилась всего лишь на миг и тут же навсегда исчезла. Напротив, здесь человек может удерживать частицу стабильно и смотреть на нее столько, сколько захочется. Точнее, столько, сколько требуется кубитам для выполнения алгоритмов квантовых вычислений.

На сегодняшний день, в частности, время удержания фермиона Майораны в Делфте исчисляется уже минутами. Для работы квантового компьютера этого обычно вполне достаточно. Так что делфтскому институту QuTech для закрепления успеха осталось сконструировать из своей квазичастицы практичный топологический кубит и обеспечить таким кубитам квантовую сцепленность для формирования когерентной вычислительной системы.
Все это, ясное дело, в высшей степени непростые технологические проблемы. Но для решения именно этих задач на подмогу к QuTech и пришла ныне корпорация-гигант Intel – со своими ресурсами, инженерами и инвестициями в размере 50 миллионов долларов. Так что все тут, практически наверняка, должно склеиться.
⇡#Намного больше, чем просто сюрпризы
Любой обзорный рассказ о прогрессе топологических квантовых компьютеров окажется заведомо неполным, если не упомянуть – хотя бы в нескольких фразах – и один чрезвычайно важный аспект в нынешней картине развития фундаментальной теоретической физики. Ибо аспект этот напрямую связывает успехи очевидно прикладных задач квантовых вычислений и сугубо теоретические – почти метафизические – изыскания науки относительно наиболее глубоких и загадочных механизмов в основе устройства природы.
Ибо чем дальше, тем больше получают теоретики такие свидетельства, которые совершенно определенно указывают на основополагающую роль информации в основе работы всей квантовой физики. Первые сигналы о начале постижения этой важнейшей взаимосвязи стали поступать еще на заре 1990-х годов – когда патриарх теоретической физики Джон Уилер (отец термина «черные дыры») впервые изрек свою афористичную формулу It from bit, то есть «Все в этом мире из битов».
Поначалу, естественно, очень многие не восприняли Уилера всерьез, особенно исследователи в области частиц высоких энергий, со времен создания атомной бомбы привыкшие считать именно себя наиболее передовым авангардом физики. Но время шло, содержательные результаты нарабатывались, и постепенно все больше и больше ученых убеждалось, сколь плодотворно и гармонично квантовая физика и теория информации дополняют друг друга – словно это разные стороны одного и того же.
И случилось так, что при подобных раскладах квантовые компьютеры и лежащий в их основе феномен квантовой сцепленности все чаще и чаще стали оказываться в фокусе междисциплинарных изысканий, которые неожиданно для всех обнаруживают глубинное единство природы в эквивалентности математических описаний для совершенно разных, казалось бы, вещей.

В эквивалентности таких, скажем, объектов, как черные дыры Вселенной (частицы макрокосмоса) и элементарные частицы материи (черные дыры микромира). В эквивалентности сильных ядерных взаимодействий в глубинах атома и слабых гравитационных взаимодействий на гигантских расстояниях космоса. В эквивалентности сугубо квантового феномена ЭПР (мгновенное взаимодействие сцепленных частиц на любых расстояниях) и межпространственного космического туннеля, «моста ЭР», связывающего сколь угодно разнесенные концы вселенной...
Все эти открытия происходили в фундаментальной науке постепенно, и уже должны были, казалось бы, приучить сообщество к тому, что сами основы современной физики ныне существенно изменяются. Тем не менее для очень многих стало большим сюрпризом, когда осенью 2015 года Джон Прескилл, известнейший специалист по квантовой информатике, опубликовал такой вот график – с динамикой публикаций тех научных статей по физике высоких энергий, которые содержат в своем названии термин Entanglement, то есть «квантовая сцепленность».

Для того, чтобы и неспециалистам стала понятна поразительная суть этой диаграммы, демонстрирующей стремительный взлет темы Entanglement, достаточно лишь пояснить, что на протяжении всего XX века очень тонкий (и для многих в ту пору крайне сомнительный) феномен квантовой сцепленности в физике высоких энергий не фигурировал вообще никак. Да и сегодня, в общем-то, к экспериментам с ускорителями-коллайдерами эта тема никакого отношения не имеет.
И тем не менее стремительный рост статей об Entanglement именно в этой секции библиотеки препринтов Arxiv.org наглядно свидетельствует о том, что и здесь теоретики всерьез занялись изучением квантово-информационных аспектов своей науки. Ну а разработчики квантовых компьютеров, в свою очередь, понемногу начинают обнаруживать, что как бы «придуманные ими самими» технические хитрости – вроде неабелевых энионов плоского 2D-мира – в других областях исследований выявляются на фундаментальных, «самых нижних» уровнях устройства природы...
В частности, сейчас имеются по меньшей мере три существенно разных разработки (от весьма известных в физике людей), указывающих на то, что при мельчайших масштабах уровня планковских длин (10-35 м) наше пространство имеет размерность 2. А затем, по мере нарастания масштаба, размерность быстро нарастает до привычных всем четырех измерений пространства-времени.
Более того, в смежной области исследований получены столь же интересные результаты (от «отца энионов» Фрэнка Вильчека), описывающие конкретный математический механизм для порождения в природе настоящих «кос», вытягивающихся за системами частиц в квантовом мнимом времени – как их материальная «мировая линия»... И есть интересные свидетельства тому, что это не только квантовая память частиц природы, но и одновременно основа Mind-Stuff – то есть «материи разума» Вселенной, пользуясь известным термином от Уильяма Кингдона Клиффорда.
Но это все, конечно же, отдельная тема для совсем другого большого рассказа.
отсюда
Поделиться: